Путь к звёздам

Мой путь к звёздам – это о том, как я пытался в словах и числах найти красоту, такую же, как и у звёзд на небе! И не только пытался, я иду по этому пути и сейчас.

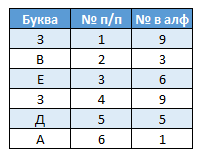
Ещё в детском саду нас (по крайней мере, меня) научили считать и читать. И я узнал, что в русском алфавите 33 буквы. Все буквы в алфавите расположены в определённом порядке, который так и называют «алфавитный порядок».

Получается, что у каждой буквы есть свой номер. На базе этого знания давным-давно был придуман простейший шифр, который называется A1Z26 или в русском варианте А1Я33. В нём буквы алфавита заменяются на их порядковые номера.

Например, слово «ЗВЕЗДА» можно зашифровать как последовательность 9-3-6-9-5-1. Про такой шифр я узнал из книжки "Мастерская головоломок", 1964 [4Mb, djvu]

После прочтения этой книги у меня в голове всегда крутились разные мысли о том, как бы так «зашифровать» какое-нибудь слово новым хитрым шифром, а именно, превратив его в рисунок. Итак, слово «звезда». Что с ним такого можно сделать? Инструментарий для «понимания» появился у меня только в средней школе, когда нас научили понятию «функция» и научили строить их графики.

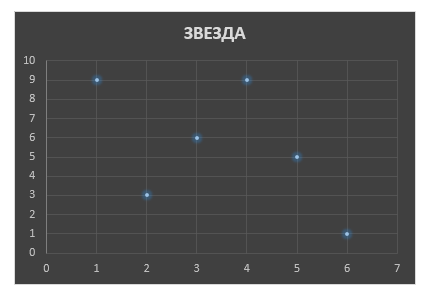
Итак, у меня была табличка с шестью дискретными значениями. Для начала я просто попробовал отобразить их на графике в виде точек.

Если делать грамотно и сейчас, то можно построить в экселе точечную диаграмму. Это, в общем-то, то же самое, что и на бумажке :))

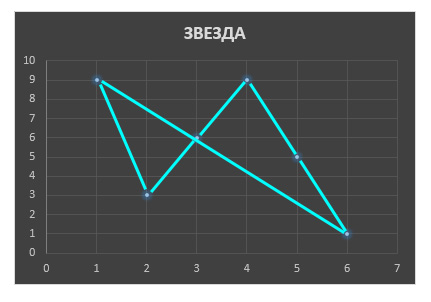
Эти точки прям как звёзды в небе, напомнило мне созвездие. А как обычно рисуют созвездия? Самые яркие их звёзды соединяют линиями. Все знают «ковш» Большой Медведицы и W Кассиопеи. Я попробовал и здесь так соединить.

Затем стал пробовать проводить линии как-нибудь по-другому. Если начать в нулевой точке, затем пройтись по порядку по всем точкам и закончить снова в нулевой точке, то получится «нулевой контур».

А если нулевую точку не привлекать, а начинать с первой буквы, то получится «первичный контур»:

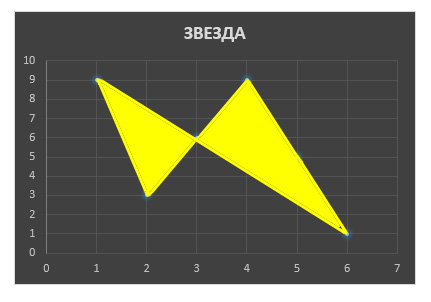
Затем я стал пробовать закрашивать получившиеся фигуры.

В принципе, уже получалось довольно красиво. Но хотелось получить что-то прям очень красивое, идеальное. Вспомнил, что вот в калейдоскопе вроде насыпаны разные кусочки стекляшек, а картинка получается симметричная. Значит, надо попробовать получившуюся фигуру каким-нибудь образом «отзеркалить». Для начала продублировал по четырём осям с поворотом на 90°.

Разве можно подумать, что такими фигурами зашифрованы слова?

Но это ещё не всё. Попробовал добавить больше «зеркальности» – наложил получившиеся фигуры сами на себя, но отзеркаленные.

Выглядит очень красиво, но из-за наложения потерялась информация, в таком виде «прочитать» зашифрованное слово будет невозможно, а ведь всё же хотелось не потерять изначальную информацию. А значит, решение получилось всё же не очень красивым.

Попробовал накладывать другим цветом и с прозрачностью:

Получилось похоже на военные кресты и ордена :)

Это сейчас я всё рисую на компьютере при помощи экселя и фотошопа, либо программирую на яваскрипте или питоне. А раньше я всё это вручную рисовал. В основном, я тренировался на кошках именах своих одноклассников и одногруппников (потому что продолжал заниматься такими вещами даже в институте).

NB: кстати, идея для бизнеса: можно делать именные медальоны :)

Следуя такой же идеологии я на javascript запрограммировал звёздные часы. Вычисляется время в формате ЧЧ:ММ:СС:мс, всего 9 цифр (для миллисекунд три цифры). Далее цифры «звездятся», замыкаясь по нулевому контуру и повторяются 4 раза с поворотом на 90°, а затем сами на себя зеркалятся. За счёт того, что это единый массив точек, составляющий один полигон, при раскраске используется интересный алгоритм «инвертирования» накладывающихся друг на друга частей. В результате при наложении информация не теряется и у многоугольника вместо сплошной получается «шахматная» раскраска.

<canvas id="canvas1"  width="280" height="280"></canvas>
 
<script>
function draw1() {
  ctx1.globalAlpha = 0.6; ctx1.fillStyle = '#fff'; ctx1.fillRect(0,0,xx,yy); 
  ctx1.beginPath(); ctx1.fillStyle='#f00'; ctx1.strokeStyle="#800"; ctx1.lineWidth=3;
 
  dat=new Date(); s=""+(((s=dat.getHours())<10)?"0"+s:s)+(((s=dat.getMinutes())<10)?"0"+s:s)
    +(((s=dat.getSeconds())<10)?"0"+s:s)+(((s=dat.getMilliseconds())<10)?"00"+s:((s>100)?s:"0"+s));
 
  for(i=0;i<160;i+=20) {p[i]=0; p[i+1]=0;}
  for(i=1;i<10;i++) { smy=parseInt(s.substr(i-1,1))*my; imx=i*mx; i2=i*2;
    p[i2    ]= imx; p[i2+  1]=-smy;
    p[i2+ 20]= imx; p[i2+ 21]= smy;
    p[i2+ 40]=-imx; p[i2+ 41]=-smy;
    p[i2+ 60]=-imx; p[i2+ 61]= smy;
    p[i2+ 80]= smy; p[i2+ 81]=-imx;
    p[i2+100]= smy; p[i2+101]= imx;
    p[i2+120]=-smy; p[i2+121]=-imx;
    p[i2+140]=-smy; p[i2+141]= imx;
  }
  ctx1.moveTo(p[0]+d,p[1]+d); for(i=2;i<p.length-1;i+=2) {ctx1.lineTo(p[i]+d,p[i+1]+d)} ctx1.stroke(); ctx1.fill();
}
  var canvas1=document.getElementById("canvas1"), ctx1=canvas1.getContext('2d'), d=130, xx=yy=d*2, mx=5, my=15;
  setInterval('draw1()',100);
</script>

Если использовать разные полигоны, разбить точки на группы и сделать полупрозрачность, тогда инвертирования не будет, но будет более красочно :)

В калейдоскопе обычно расположены три длинных зеркала, перед которыми при вращении пересыпаются всякие цветные кусочки. На просвет из-за многократного отражения и повторения получаются изумительные и завораживающие узоры. Можно попытаться изобразить слова в калейдоскопном стиле.

Обычно калейдоскоп устроен следующим образом:

Физически у нас есть одно треугольное окно, в котором видно нечто. И это нечто потом отражается в трёх зеркалах. Чтобы повторить программно, нужно будет сначала как-то нарисовать наше слово в треугольнике, после отразить его на шестиугольной сетке, а потом уже замостить ею всю плоскость.

…

У снежинок, в отличие от крестов и «звезд», получившихся выше, шестилучевая симметрия. А значит, что первичный или нулевой контур надо поворачивать не 4 раза по 90°, а 6 раз по 60°. При этом надо обязательно дополнительно зеркалить. Ну потому что снежинки, они прям симметричные-симметричные, с осевой симметрией, а не центральной.

В общем-то, снежинки могут легко получиться из калейдоскопа, если в начальном треугольнике заполнять не все три стороны, а только две.

…

Если взять «контурную» идею отображения, только вместо графика значений букв ходить по реальным путям, то получим «звёздные пути». Что за реальные пути такие? А вот какие. Например, путь обхода конём шахматной доски. Или последовательный обход чисел в волшебном квадрате.

Когда-то я уже использовал похожие технологии при рисовании ёлочек

…